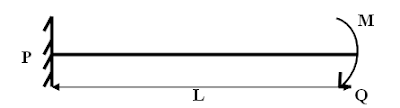
SLOPE AND DEFLECTION FOR A CANTILEVER BEAM SUBJECTED TO EXTERNAL MOMENT

SLOPE AND DEFLECTION FOR A CANTILEVER BEAM SUBJECTED TO EXTERNAL MOMENT

Fig 1

Fig 2

Consider a cantilever beam PQ of length L subjected to external moment M on the free end side of the beam.

Fig 2 show the M/EI diagram for the beam subjected to external moment. The effect of moment remains same throughout the beam; hence there is invariability in M/EI diagram.       

Slope at the free end = Area of M/EI diagram

ϴ_Q = (L) (-M/ EI)

ϴ_Q = (-ML/ EI)

Deflection at Q = (Area of M/EI diagram) (Centroidal distance from Q to O)

Y_{Q =} (L) (-M/ EI) (1/2L)

Y_Q= -ML²/2EI

Y_Q= ML²/2EI (downward direction)

SLOPE AND DEFLECTION FOR A CANTILEVER BEAM SUBJECTED TO UNIFORMLY DISTRIBUTED LOAD THROUGHOUT THE ENTIRE SPAN

SLOPE AND DEFLECTION FOR A CANTILEVER BEAM SUBJECTED TO UNIFORMLY DISTRIBUTED LOAD THROUGHOUT THE ENTIRE SPAN

Fig 1

Fig 2: M/EI diagram

Consider a cantilever beam subjected PQ (shown in fig 1) of span L, subjected to uniformly distributed load of w/m throughout the entire span. Fig 2 shows bending moment diagram of the cantilever beam with uniformly distributed load throughout the span.

Slope at the free end = Area of M/EI diagram (As per 1^st moment area theorem)

Area of parabolic diagram = (1/3) (base) (height)

ϴ_Q = (1/3) (L) (-wL²/ 2EI)

Therefore,

ϴ_Q = -Wl³/ 6EI

ϴ_Q = Wl³/ 6EI rad (clockwise with tangent from P)

Consider the M/EI diagram in which O is the centroid point and X is the distance from free end to centroid (O) of the diagram.

Deflection at a point = Product of Area of M/EI diagram and its centroidal       

                                     distance from the reference point.

Here reference point is a point on which deflection has to be determined.

Therefore,

Deflection at Q = (Area of M/EI diagram)(Centroidal distance from Q to O)

Y_{Q =} (1/3) (L) (wL²/ 2EI)(X)

Y_{Q =} (1/3) (L) (wL²/ 2EI)(3/4(L))

Y_Q= -wL⁴/8EI

Y_Q= wL⁴/8EI (downward direction)

SLOPE AND DEFLECTION FOR A CANTILEVER BEAM SUBJECTED TO POINT LOAD AT FREE END

SLOPE AND DEFLECTION FOR A CANTILEVER BEAM SUBJECTED TO POINT LOAD AT FREE END

Fig 1

Fig 2: Deflected shape of beam

Fig 3: M/EI diagram of a beam

Consider a cantilever beam PQ (fig 1) of span L subjected to point load of magnitude W KN at free end. Fig 2 shows the deflected shape of the beam.Fig 3 shows bending moment diagram of the cantilever beam with concentrated load. Let ϴ be the slope and y is the deflection for the deflected beam.

Slope at the free end = Area of M/EI diagram (As per 1^st moment area theorem)

ϴq= ½ (L) (-WL/EI)

Therefore,

ϴ_q = (-WL²/2EI)

ϴ_q = (WL²/2EI)(Clockwise with tangent from P)

Consider the M/EI diagram in which O is the centroid point and X is the distance from free end to centroid (O) of the diagram.

Deflection at a point = Product of Area of M/EI diagram and its centroidal        

                                     distance from the reference point.

Here reference point is a point on which deflection has to be determined.

Therefore,

Deflection at Q = (Area of M/EI diagram)(Centroidal distance from Q to O)

Y_{Q =} ½ (L) (-WL/EI)(X)

Y_Q= ½ (L) (-WL/EI)( 2/3(L))

Y_{Q =  -} WL³/3EI

Y_{Q =}  WL³/3EI(downward direction)

Note: Always for a cantilever beam slope and deflection is maximum in free end.